あなたは
ようこそ、米順医療統計情報クリニックホームページへ。
あなたは 番目の訪問者です!
医療統計では薬による人体への影響として最終的な判断とされる情報量(アウトカムともいいます)として寿命が比較されることがあります。寿命つまり生存時間の変化を解析する方法として最近、Coxの比例ハザードモデルが多く用いられるようになってきました。そして、多変量(この多変量は結果がたくさんあると言うことではなく、一つの結果を説明する変数がたくさんあると言うことで、言い換えれば多変数と言うことです)への拡張が可能であるという理由から、多変量つまり説明するパラメータ、例えば、薬の使用、年齢、BMI(肥満度)等などを設定した解析が行われるようになってきました。多変量解析は的確に適応すればたいへん強力な方法ですが、その使用方法もすこし複雑で、注意を要します。このあたりを少しまとめてみたいと思います。
Coxの比例ハザードモデルは、回帰分析(多変量の場合は重回帰分析)の一種です。回帰分析とはデータを最もうまく説明するグラフを描くことです。
そして、このグラフの元となる式、例えばY=aX+b を統計モデルと言います。この式が直線の場合を線形モデル、直線以外の場合を非線形モデルと言います。そして、このモデルにCoxの比例ハザード式(モデル)を用いた回帰分析のことをCoxの比例ハザード回帰と言います。
ハザードとは、瞬間的な死亡率のことです。数学的に言えば、死亡割合の微分形式のことです。そして、比例ハザードとは、二群(新薬とプラセボなど)のハザードの比、つまり死亡率を比較するのに、その比較する数式を用いた回帰分析のことです。
この比例ハザード計算式(モデル)に死亡率を計算するための複数の変数(パラメータ)を用いることが、多変量比例ハザード回帰です。そして、ハザードλが
λ0(t)exp(β1x1 +β2x2 +
-- +βnxn)
の形に表されるものを言います。ここでexp(βx)は、eのβx乗、つまりeβxの別記です。
x1 ----- xnのパラメータ項には、時間を含まないこと、そして、パラメータの合算は、eの掛け算で表されます。
これは言い換えれば、λ0(t)が基準となるハザード、例えばプラセボ群のハザードを表し、薬による効果がその乗算つまり、λ0(t)*exp(βx)で、多変数(多変量)の場合はλ0(t)*eβ1x1 *eβ2x2 *eβ3x3*---*eβnxnの形で表されると言うことです。すべての変数の効果がeβxの掛け算で、しかも、その効果が時間を含みませんので、全調査期間で一定と言うことです。これはハザード比を取ると、λ0(t)が分母、分子とも共通のため消えますので、exp(βx)となり、グラフを描けば、λ0(t)のグラフを平行移動したものになります。また、そのlogを取るとβxとなります。つまり、log変換して、グラフを描くと、二つの(プラセボと新薬)の生存割合直線が平行になると言うことです。
Coxの比例ハザードモデルの詳細な話の前に、数学の世界と現実の世界の話を少ししておきたいと思います。現在最も精度のよいと言われている数学を使った理論に量子電気力学(QED)があります。その量子電気力学による電子の磁気能率の大きさ(g因子)の値と実際の現実の値は、
g/2(理論)=1.00115965218178 ± 0.00000000000077
g/2(実験)=1.00115965218073 ± 0.00000000000028
誤差は、1.3兆分の1です。
つまり、人類史上最高と言われるQEDでさえ、現実の世界の近似でしかありません。そして、現状2変数(2対問題)は、正確に解くことが出来ますが、3変数(3対問題):例えば、地球と月と太陽の間の関係は、正確に解くことが出来ません。
つまり、Coxの比例ハザードモデルをはじめとする理論、特に多変数問題である多変量解析は現実の世界の近似でしかないと言うことです。そして、一般的に変数の数が増えれば増えるほど近似の精度は悪くなります。
ここで、累積生存率の群間比較を考えてみたいと思います。
例えば5年後などのある一時点の累積生存率を比較すると、生存曲線の全体の比較とは言い難くなります。そこで、生存曲線全体を比較する方法として、瞬間死亡率を考え、その全体的に比較した総和を比較することを考えます。数学的に言うと、二群間の瞬間死亡率の差を全体にわたって積分すればよいことになります。しかし、このためには、生存曲線を表す式(モデル)を正確に定義することが必要となります。そこで、生存曲線式を正確に求めることなく、その形を規定することにより瞬間死亡率の比を全体にわたって考えようとするものが、比例ハザードモデルとなります。
λ=λ0(t)exp(β1x1 +β2x2 +
-- +βnxn)において、
この比例ハザードモデルは、exp(β1x1 +β2x2 +
-- +βnxn)の部分に時間を含まないため、つまり全期間で一定であるため、積分の必要もありません。
ただ、死亡や調査からの脱落が存在するため、その調整の為何らかの変化が生じたごとに比を計算していきます。
ここで、x1を薬効、x2 、---xnをその他の説明変数とします。すると、λ0(t)は、すべての説明変数が0の場合を表し、それがプラセボ群を表します。そして、新薬群は、すべての説明変数が1の場合を表しています。言い換えれば、薬効以外の変数は、プラセボ群に影響力を持ってはいけない変数でなければいけません。また、λ0(t)または、λ(t)を積分して、マイナスを付ければ生存関数となることから、λ0(t)を積分した基準生存関数S0(t)を使って、他の変数の0,1の生存関数を予測することが可能です。ところが、S0(t)を求めるのが難しいため、カプラン・マイヤー法など他の方法で、求めた生存関数をS0(t)として、予想したりしますが、これには最深の注意が必要です。つまり、S0(t)は、すべての説明変数が0の場合を表さなければいけません。
また、Coxの比例ハザード回帰は、回帰分析(多変量の場合は重回帰分析)の一種です。
回帰分析は、観察量つまり、今の場合では新薬またはプラセボが、数値で表される正規分布する変数である場合にしか使えません。そこで、分類データ(つまり群A/Bの分類)の、対応のある(時間の経過を対応としてとらえる)データとして、つまり順序のある分類データをして捉えなおしたものになります。そこで、Coxの比例ハザードモデルを多変量として用いる場合は、重回帰分析の注意点が当てはまります。重回帰分析はたいへんポピュラーな手法でその長所、注意点が明確にされています。 そして、ここで問題にしなければならないものは、説明変数の独立性です。説明変数は別名、独立変数ともいいます。名前の通り、変数間は相関がない、独立な 変数であることが前提条件となっています。この独立であるとは、例えばx1を変化させた場合x1以外のパラメータに関係なく、x1のみに比例して、結果:生存割合が変わると言うことです。そして、その変化の割合は、x1以外のパラメータの値に関係なく、一定割合だと言うことです。これはまさにCoxの比例ハザードモデルの前提そのものです。この問題を重回帰分析の多重共線性と言います。
よって、Coxの比例ハザードモ デルを多変量解析として使う場合は、その説明変数がお互いに独立である必要があります。そして、プラセボ群を基準と考える場合は、説明変数がプラセボ群の結果の影響を与えてはいけないことになります。このような条件が成り立つことを比例ハザード性が成立すると言います。
一般にこのようなことは非常に特殊で、まれな場合ですので、上の条件が満たすことが明確な場合を除いて、Coxの比例ハザードモデルを多変量解析に使うことは避けるべきです。使うならば、単変量、プラセボ群と新薬群などを説明するx1のみで、使うことを考えましょう。
フィンランド症候群といわれるその論文の中にそれらしき例を見ることが出来ます。興味のある方は次を見てみてください。
(フィンランド症候群の説明へ)
簡単にまとめると
フィンランドにおいて、1974年心臓疾患による死亡への予防的介入の有効性を調べるためランダムに振り分けられた介入群(612名)とコントロール群(610名)を1919~1934年生まれの会社役員で、何らかの心臓疾患の危険因子を持つがまだ発病していない人の中から選択し、介入群には定期的な健康診断、生活習慣の指導、必要においてβアドレナリン拮抗薬、高血圧用利尿剤、高脂血症治療薬の投与の介入を5年間行い、その後21年間モニターを実施し、計26年間に及ぶ調査が行われました。その結果の原因を探るためにコックス比例ハザードモデルが使われました。その結果が次の表です。
多変量を同時に扱った影響がかなり見受けられ特に喫煙有無、1時間ブドウ糖負荷試験の値およびその信頼区間に大きな影響が表れています。このような場合は結果に疑問の余地が大きく残ります。この二つの項目が不正確な可能性が高いと言うことは、他の項目もその値に疑問が残ることになります。このようなことをよく注意したいものです。
コックス比例ハザードモデルに基づく相対リスクと95%信頼区間
| 項目 | 対照群 | 介入群 |
| 年齢 | 1.70 (1.21 - 2.37) | 1.19 (0.92 - 1.53) |
| 体重 | 0.82 (0.49 - 1.37) | 1.24 (0.85 - 1.18) |
| 最高血圧値 | 1.18 (1.00 - 1.40) | 1.02 (0.88 - 1.19) |
| コレステロール値 | 0.97 (0.79 - 1.18) | 1.08 (0.92 - 1.27) |
| 喫煙有無 | 2.78 (1.62 - 4.77) | 1.53 (1.02 - 2.30) |
| 1時間ブドウ糖負荷試験 | 1.01 (0.10 - 10.6) | 16.0 (2.53 - 100.9) |
この他にも、注意点があります。それを徐々に説明していきたいと思います。
また、時々、出来る限り多くの説明変数を入れることが良いことであるような説明を見受けますが、そこの問題があることは明確です。つまり、出来る限り少ない変数で適応すべきです。
生存曲線を使った検定として、ログランク検定がしばしば用いられます。
ログランク検定も、実際に死亡数と死亡数期待値の差を検定しますが、その差を標準化したものが正規分布をすることを前提とする、比例ハザード回帰、コックス・マンテル検定に対し、差の平方を死亡数期待値で割った値が、χ2分布することを利用して検定します。よって、χ2検定と同様に、3群以上でも検定することが出来ます。
そして、実際に死亡者数(Diとおきます)と死亡者数期待値(Di^とおきます)を群ごとに合計します。
この死亡者数と死亡者数期待値の差の平方を死亡者数期待値で割った値を全群に渡って合計すると、
χ2 = Σ{ (Di – Di^)2
/ Di^ } = (D1 – D1^)2 /
D1^ + (D2 – D2^)2 / D2^
これは、Dの死亡者数とD^の差をすべて加えた後に二乗をしていますので、全期間の平均差を二乗していることになります。
このχ2は近似的成り立つもので、特に死亡者数、または死亡者数期待値が小さい場合(一般には5以下の場合)は、近似が悪くなるとして、Yatesの補正をかけます。しかし、これはあまりうまく働かず、往々にして、あまり良くない近似となります。この誤差が大きくなる問題は一般的な問題で、群をまとめたりしますが、それが出来ない場合は、あくまで近似として取り扱うことになります。
ログランク検定にはこのような注意点があることを良く理解したうえで検定する必要があります。
Coxの比例ハザードモデルを使う場合は、特に多変量解析として使う場合は最深の注意を 払って使いましょう。 出来る限り単変量に使用を限りましょう。その結果は近似であることを研究の段階から理解し、出来る限り単純な検定が出来るように二 重盲目試験のような実験計画法に沿った、サンプルのランダム収集に注力しましょう。
ログランク検定においても同様な注意が必要です。
お問い合わせ メールを送る:
医療統計では薬による人体への影響として最終的な判断とされる情報量(アウトカムともいいます)として寿命が比較されることがあります。寿命つまり生存時間の変化を解析する方法として最近、Coxの比例ハザードモデルが多く用いられるようになってきました。そして、多変量(この多変量は結果がたくさんあると言うことではなく、一つの結果を説明する変数がたくさんあると言うことで、言い換えれば多変数と言うことです)への拡張が可能であるという理由から、多変量つまり説明するパラメータ、例えば、薬の使用、たばこ、飲酒、等などを設定した解 析が行われるようになってきました。多変量解析は的確に適応すればたいへん強力な方法ですが、その使用方法もすこし複雑で、注意を要します。このあたりを 少しまとめてみたいと思います。
Coxの比例ハザードモデルは、回帰分析(多変量の場合は重回帰分析)の一種です。回帰分析とはデータを最もうまく説明するグラフを描くことです。
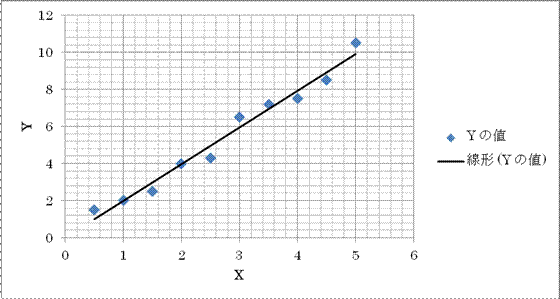
つまり、この例のように青のデータに黒のグラフを描くことです。このグラフの元となる式、Y=aX+b を統計モデルと言います。この式が直線の場合を線形モデル、直線以外の場合を非線形モデルと言います。そして、このモデルにCoxの比例ハザードモデルを用いた回帰分析のことをCoxの比例ハザード回帰と言います。
まずハザードとは、瞬間的な死亡率のことです。数学的に言えば、死亡割合の微分形式のことです。そして、比例ハザードとは、二群(新薬とプラセボなど)のハザードの比、つまり死亡率を比較することで、その比較する数式を用いた回帰分析のことです。
この比例ハザード計算式(モデル)に死亡率を計算するための複数の変数(パラメータ)を用いることが、多変量比例ハザード回帰です。そして、ハザードλが
λ0(t)exp(β1x1 +β2x2 +
-- +βnxn)
の形に表されるものを言います。ここでexp(βx)は、eのβx乗、つまりeβxの別記です。
x1 ----- xnのパラメータ項には、時間を含まないこと、そして、パラメータの合算は、eの掛け算で表されます。
これは言い換えれば、λ0(t)が基準となるハザード、例えばプラセボ群のハザードを表し、薬による効果がその乗算つまり、λ0(t)*exp(βx)で表されると言うことです。しかも、その効果が時間を含みませんので、全調査期間で一定と言うことです。
これはハザード比を取ると、λ0(t)が分母、分子とも共通のため消えますので、exp(βx)となり、グラフを描けば、λ0(t)のグラフを平行移動したものになります。また、そのlogを取るとβxとなります。つまり、log変換して、グラフを描くと、二つの(プラセボと新薬)の生存割合直線が平行になると言うことです。
Coxの比例ハザードモデルの詳細な話の前に、数学の世界と現実の世界の話を少ししておきたいと思います。現在最も精度のよいと言われている数学を使った理論に量子電気力学(QED)があります。その量子電気力学による電子の磁気能率の大きさ(g因子)の値と実際の現実の値は、
g/2(理論)=1.00115965218178±0.00000000000077
g/2(実験)=1.00115965218073±0.00000000000028
誤差は、1.3兆分の1です。
つまり、人類史上最高と言われるQEDでさえ、現実の世界の近似でしかありません。そして、現状2変数(2対問題)は、正確に解くことが出来ますが、3変数(3対問題):例えば、地球と月と太陽の間の関係は、正確に解くことが出来ません。
つまり、Coxの比例ハザードモデルをはじめとする理論、特に多変数問題である多変量解析は現実の世界の近似でしかないと言うことです。そして、一般的に変数の数が増えれば増えるほど近似の精度は悪くなります。
詳細を考えるのに次の様な例を仮定したいと思います。
|
時点1 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
10 |
0 |
10 |
0 |
|
|
B |
9 |
1 |
10 |
0.1 |
|
|
計 |
19 |
1 |
20 |
||
|
A期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|||
|
B期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|
時点2 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
9 |
1 |
10 |
0.1 |
|
|
B |
8 |
1 |
9 |
0.111 |
|
|
計 |
17 |
2 |
19 |
||
|
A期待値 |
10x17/19= 8.95 |
10x2/19= 1.05 |
|||
|
B期待値 |
9x17/19= 8.05 |
9x2/19= 0.95 |
|
時点3 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
8 |
1 |
9 |
0.111 |
|
|
B |
8 |
0 |
8 |
0 |
|
|
計 |
16 |
1 |
17 |
||
|
A期待値 |
9x16/17= 8.47 |
9x1/17= 0.53 |
|||
|
B期待値 |
8x16/17= 7.53 |
8x1/17= 0.47 |
この三つの表の様に、各時点で期待値を求めそれぞれとの差を取るのがCoxの比例ハザード回帰で使われる一般的な方法です。
表は次の様に群ごとに分けて、それぞれの群での期待値を求めることもできます。これについては、後述します。
|
群A |
時点 |
生存 |
生存期待値 |
死亡 |
死亡期待値 |
計 |
瞬間死亡率 |
|
1 |
10 |
10x19/20= 9.5 |
0 |
10x1/20= 0.5 |
10 |
0 |
|
|
2 |
9 |
10x17/19= 8.95 |
1 |
10x2/19= 1.05 |
10 |
0.1 |
|
|
3 |
8 |
9x16/17= 8.47 |
1 |
9x1/17= 0.53 |
9 |
0.111 |
Coxの比例ハザードモデルは、多変量(多変数)も扱うことが出来ますが、煩雑なのでとりあえず上記のような各時点の2x3の分割表を考えてみます。
これは、連続する期間でA群とB群を観察して、時点1、B群で死亡者1名、時点2、A群で死亡者1名、B群で死亡者1名、さらに時点2、A群で死亡者1名のイベントが発生した状況を考えて、生存曲線などを考えてみたいと思います。
この2x3の分割表の場合には、内容はコックス・マンテル検定とほとんど同等となります。
分割表を一般化して、いつものように次の形にしたいと思います。
|
説明変数 |
結果 |
||||
|
群 |
B1:生存 |
B2:死亡 |
Ai小計 |
P(Ai) |
|
|
A1 |
a |
b |
a+b (固定) |
(a+b)/ |
|
|
A2 |
c |
d |
c+d (固定) |
(c+d)/ |
|
|
Bi小計 |
a+c (固定) |
b+d (固定) |
a+b+c+d (固定) |
||
|
P(Bi) |
(a+c)/ |
(b+d)/ |
|||
注)P(Ai)は、Aiの確率を表します。
ここで、興味のあるものは生存割合、またはその逆の死亡割合です。その割合を求めるのに、まず次のことを考えてみます。
赤球 N0 個,白球 N1 個入っている袋から,n 個取出すとき,その n 個の中の赤球の個数 X
の分布は,超幾何分布 H(N,N0,n)(ここで,N=N0+N1 とし、またAとBの小計は固定とする)
F(x) = N0Cx ・N1Cn-x /NCn {
max(0, n-N1) ≦ x ≦ min(n,N0) }
この超幾何分布は、個数が多くなると二項分布に近づきます。
これを上記表に当てはめてみますと、全体a+b+c+dから、死亡者小計b+dを取り出すときの、A1群の死亡者数がbである。言い換えると、a+b+c+d人の内、b+d人が死亡するとの状況の中で、A1群からb人死亡する確率を表します。
そして、この2x2の分割表は、自由度が1ですので、一か所の値が求まれば、他は決まります。
瞬間死亡率を最終的には求めたいので、死亡割合を考えます。その標準誤差、つまり期待値からの隔たりを求めてみます。
上の項目bの期待値は、(a+b)(b+d)/(a+b+c+d)です、そして、bとの差ですので、標準誤差は
b - (a+b)(b+d)/(a+b+c+d)
です。そして、これは一時点の値ですので、それぞれの時点のこの値をすべての表に渡って加え合わせる必要があります。そして、これは加算するほどどんどん大きくなってしまいますので、そのサンプル数で割っておきます。また、時間の順番を区別するためにkの添え字を使い、今後の為にJと置いておきます。すると、
Jk = bk – (ak+bk)(bk+dk)
/ (ak+bk+ck+dk) = bk – nk1mk2
/ Nk
nk1 = ak+bk
、mk2 = bk+dk 、Nk = ak+bk+ck+dk
となります。
すると、標準偏差を求める式の分子Jは、
J = ΣJk =Σ(bk – nk1mk2
/ Nk)
生存曲線を求めたいため、死亡割合にマイナスをかけておきます。よって、
J = ΣJk = -Σ(bk – nk1mk2
/ Nk)
この分母は、全体の偏り具合を表す量が必要ですので、分母をIとすると
I =Σ((ak+ck)(bk+dk)
(ak+bk)(ck+dk) / (ak+bk+ck+dk)
(ak+bk+ck+dk) (ak+bk+ck+dk-1))
=Σ(mk1 mk2
nk1 nk2 / (Nk) (Nk) (Nk
-1))
コックスのβ = J/I
βの標準誤差:SE(β)=√(1/I)
ハザード比(A2群/A1群):HR = exp(β)
ここまでは、超幾何分布ですが、なぜか信頼区間、検定の際は正規分布を仮定して次のように計算します。
z0 = |β|/SE(β)=|J/I|/|√(1/I)|=|J|/|√(I)|
|z0| >= t(∞、0.05)にて、0.05%有意水準の正規分布を仮定した、検定をします。
同様に、正規分布仮定の信頼区間は、
βL = β – t(β,0.05)xSE(β) :95%信頼区間下限
βH = β + t(β,0.05)xSE(β):95%信頼区間上限
となります。
ここで、注意すべきは期待値がnk1mk2
/ Nkで表されると言うことです。つまり、k時点と言う、一観測時点から求められる値が期待値になっている、時間概念が期待値に入っていないと言うことです。
これらを時点1、時点2、時点3に適応してみますと、
|
時点1 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
10 |
0 |
10 |
0 |
|
|
B |
9 |
1 |
10 |
0.1 |
|
|
計 |
19 |
1 |
20 |
||
|
A期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|||
|
B期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|
時点2 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
9 |
1 |
10 |
0.1 |
|
|
B |
8 |
1 |
9 |
0.111 |
|
|
計 |
17 |
2 |
19 |
||
|
A期待値 |
10x17/19= 8.95 |
10x2/19= 1.05 |
|||
|
B期待値 |
9x17/19= 8.05 |
9x2/19= 0.95 |
|
時点3 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
8 |
1 |
9 |
0.111 |
|
|
B |
8 |
0 |
8 |
0 |
|
|
計 |
16 |
1 |
17 |
||
|
A期待値 |
9x16/17= 8.47 |
9x1/17= 0.53 |
|||
|
B期待値 |
8x16/17= 7.53 |
8x1/17= 0.47 |
J = ― (0 – 10x1/20) –
(1 – 10x2/19) – (1 – 9x1/17) ≒ 0.08204
I = 19x1x10x10/(20x20x19) + 17x2x10x9/(19x19x18) + 16x1x9x8/(17x17x16) ≒0.9700
β = 0.08204/0.9700
≒0.08458
χ2 = 0.082042/0.9700
= 0.00694
SE(β) = √(1/0.08458) ≒ 3.438
βL = β – t(β,0.05)xSE(β) = 0.08458 – 1.96x3.438 = -5.708 :95%信頼区間下限
βH = β + t(β,0.05)xSE(β) = 0.08458 + 1.96x3.438 = 6.638: 95%信頼区間上限
Z0 = 0.08458/3.438 ≒ 0.0246 < t(∞、0.05)=1.96 有意水準5%で有意でない。
exp(β)=1.088:ハザード比
χ2にイエーツ(Yates’)の補正を適応すると、
χ2(Yates ‘) =
(0.08204 – 0.5)2/0.9700 = 0.1801
この方法をマンテル・ヘンツェル(Mantel-Haenstzel)法 / コクラン・マンテル・ヘンツェル(Cochran-Mantel-Haenstzel)法に元づいた、ログランク検定と言います。
Cox比例ハザード回帰は、各パラメータの寄与率βを求めることに重きが置かれ、検定が必要な場合は、このログランク検定(MH)または、後ほど説明するχ二乗をそのまま応用した(超幾何分布に基づくのではなく)ログランク検定を使います。
ここで重要な注意点があります。この計算の中には、時間の概念が含まれていません。
時点1が起こった後に、時点2が起こる事実のみを使用しています。時点1と時点2がどの程度時間的に離れているかが組み込まれていません。これでは、せっかく生存曲線を時間軸に対して測定、描画したのに意味がありません。改善が望まれ、改善案が出ていますが、これはというものはありません。この点からいっても、Coxの比例ハザード解析はアイデアを得るための方法である場合がほとんどです。出来る限り単純な条件で、最深の注意を払って使用すべきです。x1のみの単変数ならば、注意深く使用すれば有意義な結果が注質出来る可能性があります。
今の様々な計算は各時点で、期待値との差をとり加算したものでした。これが、一般的です。
しかし、これは、全期間でハザードが一定であるとの強い制約のもとでの計算でした。この制約に合致しそうかは、グラフを描けば雰囲気は分かりますが、数値計算をする方法として、それぞれの群ですべてのデータを下の様にまとめ、期待値をこちらのテーブルから計算し、同様な計算をすることが可能です。こちらの期待値は、時点ごとの表からの期待値ではなく、群AまたはBの全区間における死亡者数の平均値が期待値とされる違いがあります。つまり、全期間での期待値です。
これはあくまで、参考情報でしかありませんが、考える材料とはなり得ます。
|
群A |
時点 |
生存 |
生存期待値 |
死亡 |
死亡期待値 |
計 |
瞬間死亡率 |
|
1 |
10 |
10x19/20= 9.5 |
0 |
10x1/20= 0.5 |
10 |
0 |
|
|
2 |
9 |
10x17/19= 8.95 |
1 |
10x2/19= 1.05 |
10 |
0.1 |
|
|
3 |
8 |
9x16/17= 8.47 |
1 |
9x1/17= 0.53 |
9 |
0.111 |
χ2(異質性) =χ2(全体) -χ2(独立性)
より、まずχ2(全体)を求めます。実際には、死亡者数のみを使用します。
χ2(全体)
= (0 – 10x1/20)2/10x1/20 + (1 – 10x2/19)2/10x2/19
+ (1 – 9x1/17)2/9x1/17
= 10x20/(20x20x10) + 2x19/(19x19x10) + 6x17/(17x17x9)
= 1/20 + 1/(5x19) + 2/(3x17)
= 0.09974
χ2(独立性) = J2/I =0.00694
この場合は、Yatesの補正を含まない方を使用します。
よって、
χ2(異質性) =χ2(全体) -χ2(独立性) = 0.09974 – 0.00694 = 0.0928
コクランのQ検定がよく、異質性に用いられますが、それは、次のように表を変更し、
|
群 |
時点1 |
時点2 |
時点3 |
計 |
|
A |
1 |
1 |
0 |
2 |
|
B |
0 |
1 |
1 |
2 |
|
計 |
1 |
2 |
1 |
4 |
J = (2-1){2(22 + 22) – (2+2)2} =
1x(2x8 – 16) = 0
I = {2(1+2+1) – (12+22+12)} = 2x4 – 6
= 2
Q =J/I = 16/6 = 0.0 < χ2(2) = 5.991
つまり、異質性は有意ではない。
つまり、最初のχ2値(独立性)が大きいと、二つの群AとBは、明確な有意差があることを表し、二つ目のχ2(異質性)が小さいと、ハザード比のばらつきが小さいことを表します。何らかの指標がほしい場合には使ってもよいかもしれません。
そして、このβが0であるかの検定をコックス・マンテルの検定と呼び、単変量の比例ハザード回帰と同じになります。
そして、exp(β)=1.088のことをハザード比と呼び、HRと表すことが多いようです。
このハザード比は、概念的には、オッズ比と同じであり、この解釈には注意が必要です。ハザード比は、1.088倍となりますが、実際には、2/10と2/10の違いで0です。ハザード比も本来は絶対割合で比較すべきです。
先ほど マンテル・ヘンツェル法に元づいた、ロングラン検定の計算で、それぞれにサンプル数をかけたものを一般化Wilcoxson検定と言います。つまり、
J(MH) = ― (0 – 10x1/20) –
(1 – 10x2/19) – (1 – 9x1/17) ≒ 0.08204
であったものを
J(WC) = ― 20x(0 –
10x1/20) – 19x(1 – 10x2/19) – 17x(1 – 9x1/17)
= – (0 – 10) – (19 – 20) –
(17 – 9) = 10 + 1 – 8 = 3
I(MH) = 19x1x10x10/(20x20x19) + 17x2x10x9/(19x19x18) +
16x1x9x8/(17x17x16) ≒ 0.9700
であったものを
I(WC) = 20x20x19x1x10x10/(20x20x19) + 19x19x17x2x10x9/(19x19x18) + 17x17x16x1x9x8/(17x17x16)
= 10x10 + 17x10 + 9x8 = 342
χ2 (MH)= 0.082042/0.9700
≒ 0.00694
であったものが
χ2(WC) =
J(MH)2/I(MH) = 3x3/342 ≒ 0.026316
χ2(MH) (Yates ‘) =
(0.08204 – 0.5)2/0.9700 = 0.1801
であったものが
χ2(WC) (Yates ‘) =
(3x3 – 0.5)2/342 = 0.02485
ただ、この場合各期待値の値が5を超えますので、補正しないのが一般的です。
生存曲線を使った検定として、ログランク検定がしばしば用いられます。
ログランク検定も、実際に死亡数と死亡数期待値の差を検定しますが、その差を標準化したものが正規分布をすることを前提とする、比例ハザード回帰、コックス・マンテル検定に対し、差の平方を死亡数期待値で割った値が、χ2分布することを利用して検定します。よって、χ2検定と同様に、3群以上でも検定することが出来ます。
そして、死亡者数期待値は、同様にnk1mk2
/ Nk、nk2mk2
/ Nkとなります。そして、実際に死亡者数(Diとおきます)と死亡者数期待値(Di^とおきます)を群ごとに合計します。つまり、
D1 =Σbk = b1
+ b2
D2 =Σdk = d1
+ d2
D1^ =Σnk1mk2
/ Nk = n11m12 / N1 + n21m22
/ N2
D2 ^=Σnk2mk2
/ Nk = n12m12 / N1 + n22m22
/ N2
この死亡者数と死亡者数期待値の差の平方を死亡者数期待値で割った値を全群に渡って合計すると、
χ2 = Σ{ (Di – Di^)2
/ Di^ } = (D1 – D1^)2 /
D1^ + (D2 – D2^)2 / D2^
これは、Dの死亡者数とD^の差をすべて加えた後に二乗をしていますので、全期間の平均差を二乗していることになります。
このχ2は近似的成り立つもので、特に死亡者数、または死亡者数期待値が小さい場合(一般には5以下の場合)は、近似が悪くなるとして、イェーツ(Yates’)の補正をかけます。しかし、これはあまりうまく働かず、往々にして、あまり良くない近似となります。この誤差が大きくなる問題は一般的な問題で、群をまとめたりしますが、それが出来ない場合は、あくまで近似として取り扱うことになります。
ログランク検定にはこのような注意点があることを良く理解したうえで検定する必要があります。
先ほどの例で、実際に計算してみたいと思います、先ほどの表を再度用います。
|
開始時点 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
10 |
0 |
10 |
0 |
|
|
B |
10 |
0 |
10 |
0 |
|
|
計 |
20 |
0 |
20 |
|
時点1 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
10 |
0 |
10 |
0 |
|
|
B |
9 |
1 |
10 |
0.1 |
|
|
計 |
19 |
1 |
20 |
||
|
A期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|||
|
B期待値 |
10x19/20= 9.5 |
10x1/20= 0.5 |
|
時点2 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
9 |
1 |
10 |
0.1 |
|
|
B |
8 |
1 |
9 |
0.111 |
|
|
計 |
17 |
2 |
19 |
||
|
A期待値 |
10x17/19= 8.95 |
10x2/19= 1.05 |
|||
|
B期待値 |
9x17/19= 8.05 |
9x2/19= 0.95 |
|
時点3 |
群 |
生存 |
死亡 |
計 |
瞬間死亡率 |
|
A |
8 |
1 |
9 |
0.111 |
|
|
B |
8 |
0 |
8 |
0 |
|
|
計 |
16 |
1 |
17 |
||
|
A期待値 |
9x16/17= 8.47 |
9x1/17= 0.53 |
|||
|
B期待値 |
8x16/17= 7.53 |
8x1/17= 0.47 |
D1 = 0 + 1 + 1 = 2
D1^ = 0.5+1.05+0.53 = 1.63
D2 = 1 + 1 + 0 = 2
D2^ = 0.5 + 0.95 + 0.47 = 1.92
χ2 = Σ{ (Di – Di^)2
/ Di^ } = (D1 – D1^)2 /
D1^ + (D2 – D2^)2 / D2^
(D1 – D1^)2 / D1^
= ( 2 – 1.63 ) x ( 2 – 1.63 ) / 1.63 = 0.0840
(D2 – D2^)2 / D2^
= ( 2 – 1.92 ) x ( 2 – 1.92 ) / 1.92 = 0.0033
χ2 = 0.0840 + 0.0033
= 0.087 < 3.84(自由度1) 5%統計的有意差なし
これは、結局下の2x2の分割表の有意差検定をしていることになります。結局ログランク検定は、死亡者数、死亡者数期待値とも加算して、その後差を取っていますので、全期間に渡っての平均の値を求めていることになります。
|
群 |
死亡者数観測値 |
死亡者数期待値 |
計 |
|
A |
2 |
1.63 |
2.63 |
|
B |
2 |
1.92 |
2.92 |
|
計 |
4 |
3.55 |
7.55 |
観測値と期待値との差を0に近い側に0.5ずつ修正する
(D1 – D1^)2 / D1^
= ( 2 – 1.63 – 0.5 ) x ( 2 – 1.63 – 0.5
) / 1.63
= -0.13 x -0.13 / 1.63 = 0.0104
(D2 – D2^)2 / D2^
= ( 2 – 1.92 – 0.5 ) x ( 2 – 1.92 – 0.5
) / 1.92
= -0.42 x -0.42 / 1.92 = 0.0919
χ2 = 0.0104 + 0.0919
= 0.93 < 3.84(自由度1) 5%統計的有意差なし
どちらも結果的には、統計的有意差なしになりました。ただ、イェーツ(Yates')の補正をかけた方がχ2値は大きくなりました。結果の表を見て差がないことが理にかなっており、この修正結果は負の効果をもたらしたと考えられます。
もちろん観測期間を長くとり、データをたくさん集めていけば、この問題は改善されていきますが、これが近似的に成り立つと言われる一面です。
このような注意点を十分理解したうえで、計画段階からそれを避ける研究を計画するのが正しい方向性です。
先ほどのマンテル・ヘンツェル法に基づくログランク検定と比較してみますと
マンテル・ヘンツェル法に基づくログランク検定、ログランク検定、一般化Wilcoxson検定の結果比較
χ2 (MH) ≒ 0.00694
χ2(MH) (Yates ‘) ≒ 0.1801
χ2 (LG) ≒ 0.087
χ2(LG) (Yates ‘)
≒ 0.93
なお、一般化Wilcoxson検定は、
χ2(WC) ≒ 0.026316
χ2(WC) (Yates ‘) ≒ 0.02485
ルールに基づいて比較するならば
χ2(MH) (Yates ‘) ≒ 0.1801
χ2(LG) (Yates ‘) ≒ 0.93
χ2(WC) ≒ 0.026316
お問い合わせ メールを送る: